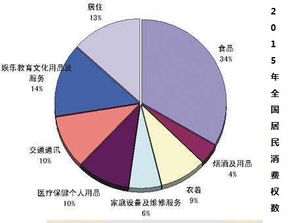
权数是什么? 权数是指在机器学习算法中,用来衡量模型预测值与真实值之间差异的权重。在训练模型时,我们通常会使用大量的数据来训练模型,而这些数据中包含了真实值的上下文信息,而模型预测的值则是根据模型的学习到的特征和模型本身的拟合能力来预测的。因此,权数的作用就是将真实值的上下文信息加入到模型预测值的计算中,从而提高模型的预测准确度。 那么,权数在具体应用中是如何计算的呢?一般来说,权数可以分为两类:一类是特征重要性权数,这类权数通常是通过对特征的统计量进行计算得到的,比如均方误差、均方根误差等;另一类是模型复杂度权数,这类权数通常是通过对模型的复杂度进行计算得到的,比如过拟合、欠拟合等。 在实际应用中,我们需要根据具体的任务和数据情况来选择合适的权数,以达到最佳的预测效果。同时,权数的选取也需要考虑到模型的可解释性,不能选择过于复杂的权数导致模型的预测不可解释。 权数是机器学习算法中一个非常重要的概念,它可以帮助我们更好地理解模型的预测过程,并为模型的训练和应用提供重要的参考信息。 --- 权数在机器学习中的作用及计算方法 权数是机器学习算法中一个非常重要的概念,它可以帮助我们更好地理解模型的预测过程,并为模型的训练和应用提供重要的参考信息。 权数可以分为两类:特征重要性权数和模型复杂度权数。 ### 特征重要性权数 特征重要性权数通常是通过对特征的统计量进行计算得到的。这类权数通常用于回归问题中,用来衡量每个特征对预测值的影响程度。常用的特征重要性权数包括均方误差、均方根误差等。 在回归问题中,我们通常使用多元线性回归模型来建立自变量和因变量之间的关系。对于每个自变量,我们需要计算其对预测值的贡献度,通常使用权重来表示每个自变量对预测值的贡献度。而这些权重通常就是特征重要性权数。 ### 模型复杂度权数 模型复杂度权数通常是通过对模型的复杂度进行计算得到的。这类权数通常用于分类问题中,用来衡量模型的拟合能力。常用的模型复杂度权数包括过拟合、欠拟合等。 在分类问题中,我们通常使用逻辑回归模型来建立自变量和因变量之间的关系。对于每个自变量,我们需要计算其对分类结果的影响程度,通常使用权重来表示每个自变量对分类结果的影响程度。而这些权重也通常就是模型复杂度权数。 权数的选取需要考虑到模型的可解释性,不能选择过于复杂的权数导致模型的预测不可解释。 权数是机器学习算法中一个非常重要的概念,它可以帮助我们更好地理解模型的预测过程,并为模型的训练和应用提供重要的参考信息。