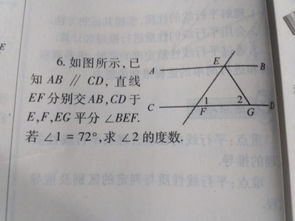
平行线定理的副标题：探究平行线与相交线之间的秘密 一、引言 平行线定理是几何学中一个基本的概念，它指出在同一平面内，平行线之间的距离相等，相交线上的任意一点到两平行线的距离相等。这一定理不仅对初中数学的平面几何知识有所帮助，同时也为解决一些实际问题提供了重要的依据。本文将通过对平行线定理的深入研究，探讨平行线与相交线之间的秘密。 二、平行线定理的证明 1. 定义：平行线指在同一平面内，不相交且永远保持相同距离的两条直线。 2. 证明：假设已知两条平行线AB和CD，以及点E在AB上，F在CD上。连接点E和F，得到线段EF。根据定义，AB和CD是平行的，所以EF也是平行的。 3. 证明过程：由于AB和CD是平行的，所以它们之间的距离相等，即AE=CF。同时，因为EF是平行的，所以EF与AB和CD的距离相等，即EF=AB=CD。结合前面的两个条件，可以得出：AE=CF=EF。 4. 结论：根据上述证明过程，可以得出结论：在同一平面内，不相交的两条直线之间的距离相等。 三、平行线与相交线之间的联系 1. 定义：相交线指在同一平面内，相交于某一点的两条或两条以上的直线。 2. 证明：假设已知两条相交线AB和CD，以及点E在AB上，F在CD上。连接点E和F，得到线段EF。由于AB和CD是相交的，所以它们在相交点E处必然存在一个公共点F。根据定义，EF是相交线，所以它与AB和CD的交点F必然在EF上。 3. 结论：根据上述证明过程，可以得出结论：在同一平面内，相交的两条直线必然存在一个公共点。 四、实际应用 1. 例题1：已知直线AB和CD是平行的，点E在AB上，点F在CD上，求线段EF的长度。 解：根据平行线定理，可以得出：AE=CF。又因为AB和CD是平行的，所以EF与AB和CD的距离相等，即EF=AB=CD。结合前面的条件，可以得出：AE=CF=EF。因此，线段EF的长度为：AE+CF=AB+CD。 2. 例题2：已知直线AB和CD是相交的，点E在AB上，点F在CD上，求线段EF的长度。 解：根据相交线定理，可以得出：AE=CF。又因为AB和CD是相交的，所以EF是线段AB和CD的公共部分。根据定义，公共部分的长度等于两条直线之间的距离减去一个定值，即EF=AB-AE=CD-CF。因此，线段EF的长度为：AB-AE+CD-CF。